SYSC5108_A3

博主： William.W
发布时间：2025 年 03 月 06 日
557 次浏览
44 条评论
12248字数
分类：代码-Code

[SYSC 5108 W25 Assignment 3.pdf](https://anime.bbmi.me/usr/uploads/2025/03/936283889.pdf)

# SYSC 5108 W25 ssignment 3

William Wang
101191168

## Q1

From the Beta–Binomial conjugacy principle, a uniform $\theta \sim \text{Beta}(1,1)$ prior combined with the Binomial likelihood (with $x$ successes out of $n$ yields a posterior distribution

$$
p(\theta \mid x) = \text{Beta}\bigl(x + 1,\; n - x + 1\bigr).
$$

## Q2

### (a)

Weighted sum = $0.20 \cdot 1 + (-0.10) \cdot 0.2 + 0.25 \cdot 0.5 + 0.05 \cdot 0.7 = 0.34$

### (b)

Threshold ($\theta = 1$) output =

$$
\begin{cases}
1 & \text{if } 0.34 \ge 1 \\
0 & \text{otherwise}
\end{cases}
$$

So output = 0.

## (c)

Logistic ($\varphi$) output =

$$
\frac{1}{1 + e^{-0.34}} \approx 0.58.
$$

## (d)

ReLU output = $\max(0,\,0.34) = 0.34.$

## Q3

### (a) Logistic (sigmoid) activation

- **Neuron 3**
  
  $a_3 = \sigma(z_3)= \tfrac{1}{1 + e^{-(1.0 \times 0.7) + (0.6 \times 0.3) + 0.1 = 0.7 + 0.18 + 0.1}} = \tfrac{1}{1 + e^{-0.98}} \approx 0.73.$
- **Neuron 4**
  
  $a_4 = \sigma(z_4)= \tfrac{1}{1 + e^{-(0.9 \times 0.7) + (-0.8 \times 0.3) + 0.5 = 0.63 - 0.24 + 0.5 }} = \tfrac{1}{1 + e^{-0.89}} \approx 0.71.$
- **Neuron 5**
  
  $a_5 = \sigma(z_5) = \tfrac{1}{1 + e^{-(0.3 \times 0.73) + (0.2 \times 0.71) + 0.9 \approx 0.219 + 0.142 + 0.9}} = \tfrac{1}{1 + e^{-1.261}} \approx 0.78.$

**Neuron 5’s output $\approx 0.78$.**

### (b) ReLU activation

- **Neuron 3**
  $a_3 = \max(0,\,0.98) = 0.98.$
- **Neuron 4**
  $a_4 = \max(0,\,0.89) = 0.89.$
- **Neuron 5**
  $a_5 = \max(0,\,1.372) = 1.372.$

Hence, **Neuron 5’s output $\approx 1.37$.**

### (c) Filling in the network diagram (ReLU case)

- **Weights and biases** :
  
  - $w_{3,1} = 1.0,\; w_{3,2} = 0.6,\; b_3 = 0.1$
  - $w_{4,1} = 0.9,\; w_{4,2} = -0.8,\; b_4 = 0.5$
  - $w_{5,3} = 0.3,\; w_{5,4} = 0.2,\; b_5 = 0.9$
- **Neuron 3**
  
  - Weighted sum: $z_3 = 1.0 \times 0.7 + 0.6 \times 0.3 + 0.1 = 0.98$
  - Activation: $a_3 = \mathrm{ReLU}(0.98) = 0.98$
- **Neuron 4**
  
  - Weighted sum: $z_4 = 0.9 \times 0.7 + (-0.8) \times 0.3 + 0.5 = 0.89$
  - Activation: $a_4 = \mathrm{ReLU}(0.89) = 0.89$
- **Neuron 5**
  
  - Weighted sum: $z_5 = 0.3 \times a_3 + 0.2 \times a_4 + 0.9 = 1.372$
  - Activation: $a_5 = \mathrm{ReLU}(1.372) = 1.372$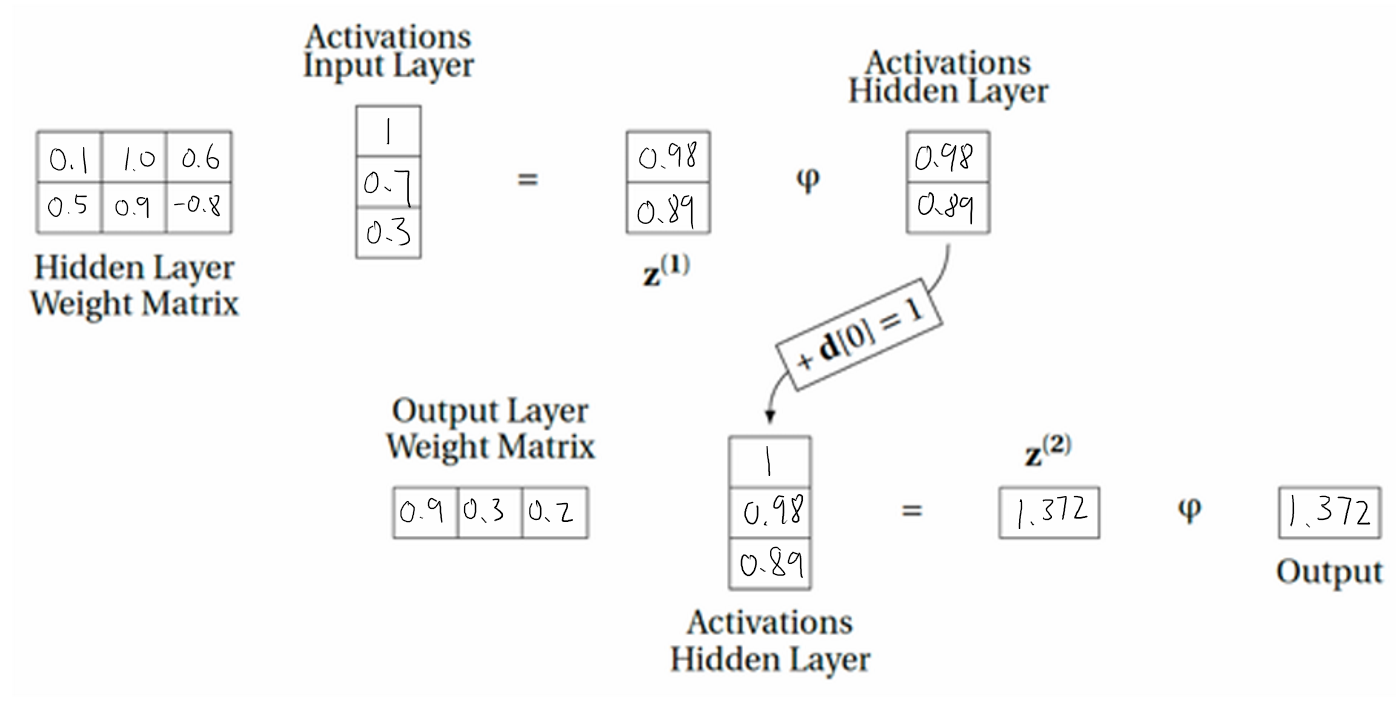

![image.png](https://anime.bbmi.me/usr/uploads/2025/03/1126946878.png)

## Q4

### (a) Network Output

$$
\begin{aligned}
&\text{Hidden neurons:} \\
&a_2 = \max(0, 0.2 \times 0.5) = 0.1, \\
&a_3 = \max(0, 0.3 \times 0.5) = 0.15, \\
&a_4 = \max(0, 0.4 \times 0.5) = 0.2. \\

&\text{Output neuron:} \\
&y = a_5 = \max\bigl(0, (0.5 \times 0.1) + (0.6 \times 0.15) + (0.7 \times 0.2)\bigr) \\
&\quad = \max(0, 0.05 + 0.09 + 0.14) \\
&\quad = \max(0, 0.28) \\
&\quad = 0.28.
\end{aligned}
$$

### (b) Error Values ($\delta$) for Each Processing Neuron

$$
E = \frac{1}{2} (t - y)^2 
  = \frac{1}{2} (0.9 - 0.28)^2
  = \frac{1}{2} (0.62)^2
  = 0.1922.
$$

### (c) Gradients of the Error w.r.t. Each Weight

$$
\delta_5 = (y - t)\cdot \mathbf{1}_{z_5>0}
          = (0.28 - 0.9)\times 1
          = -0.62.
$$

For hidden neurons $i \in \{2,3,4\}$:

$$
\delta_i = \delta_5 \times w_{5,i},
$$

thus

$$
\delta_2 = -0.62 \times 0.5 = -0.31, \quad
\delta_3 = -0.62 \times 0.6 = -0.372, \quad
\delta_4 = -0.62 \times 0.7 = -0.434.
$$

### (d) Weight Updates with $\alpha=0.1$

The gradient formulas are:

$$
\frac{\partial E}{\partial w_{5,i}} = \delta_5\,a_i, 
\quad 
\frac{\partial E}{\partial w_{i,1}} = \delta_i \, x.
$$

Output layer:

$$
\begin{aligned}
\frac{\partial E}{\partial w_{5,2}} 
&= \delta_5 \, a_2 
= (-0.62)\times0.1 
= -0.062,\\
\frac{\partial E}{\partial w_{5,3}} 
&= (-0.62)\times0.15 
= -0.093,\\
\frac{\partial E}{\partial w_{5,4}} 
&= (-0.62)\times0.2 
= -0.124.
\end{aligned}
$$

Hidden layer:

$$
\begin{aligned}
\frac{\partial E}{\partial w_{2,1}} 
&= \delta_2 \times x 
= (-0.31)\times0.5 
= -0.155,\\
\frac{\partial E}{\partial w_{3,1}} 
&= (-0.372)\times0.5 
= -0.186,\\
\frac{\partial E}{\partial w_{4,1}} 
&= (-0.434)\times0.5 
= -0.217.
\end{aligned}
$$

### (e) Recalculation of the Error with Updated Weights

With learning rate $\alpha=0.1$, each weight update is

$$
w \leftarrow w - \alpha \,\frac{\partial E}{\partial w}.
$$

Output layer:

$$
\begin{aligned}
w_{5,2}^{\text{new}} &= 0.5 - 0.1\times(-0.062) 
                    = 0.5 + 0.0062 
                    = 0.5062,\\
w_{5,3}^{\text{new}} &= 0.6 - 0.1\times(-0.093) 
                    = 0.6 + 0.0093 
                    = 0.6093,\\
w_{5,4}^{\text{new}} &= 0.7 - 0.1\times(-0.124) 
                    = 0.7 + 0.0124 
                    = 0.7124.
\end{aligned}
$$

Hidden layer:

$$
\begin{aligned}
w_{2,1}^{\text{new}} &= 0.2 - 0.1\times(-0.155) 
                     = 0.2 + 0.0155 
                     = 0.2155,\\
w_{3,1}^{\text{new}} &= 0.3 - 0.1\times(-0.186) 
                     = 0.3 + 0.0186 
                     = 0.3186,\\
w_{4,1}^{\text{new}} &= 0.4 - 0.1\times(-0.217) 
                     = 0.4 + 0.0217 
                     = 0.4217.
\end{aligned}
$$

Checking the New Error(Forward Pass with Updated Weights):

$$
\begin{aligned}
a_2' &= \max(0, 0.2155\times0.5) = 0.10775,\\
a_3' &= \max(0, 0.3186\times0.5) = 0.1593,\\
a_4' &= \max(0, 0.4217\times0.5) = 0.21085,\\
y' &= a_5' = \max\bigl(0,
       0.5062\times0.10775 + 0.6093\times0.1593 + 0.7124\times0.21085\bigr) 
    \approx 0.302.
\end{aligned}
$$

$$
E' = \frac{1}{2} (t - y')^2 
    = \frac{1}{2} (0.9 - 0.302)^2 
    = 0.1788 < 0.1922.
$$

Thus, the error has decreased, indicating successful training for this step.

## Q5

### a) What value will this network output?

Define the input:

$$
[1, 2, 3, 4, 5, 6]
$$

The first layer is a convolution with a window size of 3 and stride 1. The filter has weights:

$w_1 = 1, \quad w_2 = 1, \quad w_3 = 1 $ and a bias: $w_0 = 0.75$

Since this is a simple sum followed by a bias addition, we slide the window over the input, computing the convolution at each position.

For the first position using $[1,2,3]$:

$$
z_1 = (1 + 2 + 3) + 0.75 = 6.75
$$

$$
a_1 = \max(0, 6.75) = 6.75
$$

For the second position using $[2,3,4]$:

$$
z_2 = (2 + 3 + 4) + 0.75 = 9.75
$$

$$
a_2 = \max(0, 9.75) = 9.75
$$

For the third position using $[3,4,5]$:

$$
z_3 = (3 + 4 + 5) + 0.75 = 12.75
$$

$$
a_3 = \max(0, 12.75) = 12.75
$$

For the fourth position using $[4,5,6]$:

$$
z_4 = (4 + 5 + 6) + 0.75 = 15.75
$$

$$
a_4 = \max(0, 15.75) = 15.75
$$

At this point, the feature map after the convolutional layer is:

$$
[6.75, 9.75, 12.75, 15.75]
$$

Next, we apply max pooling with kernel size 2 and stride 2.

The first pooling window takes:

$$
\max(6.75, 9.75) = 9.75
$$

The second pooling window takes:

$$
\max(12.75, 15.75) = 15.75
$$

So, after max pooling, the output is:

$$
[9.75, 15.75]
$$

Now, these two values go into the fully connected layer. There is only one neuron, which has:

- Bias: $w_4 = 1  $
- Weights: $w_5 = 0.2, \quad w_6 = 0.5$

The neuron computes:

$$
z_7 = w_4 + w_5 \cdot 9.75 + w_6 \cdot 15.75
$$

Substituting the values:

$$
z_7 = 1 + (0.2 \times 9.75) + (0.5 \times 15.75)
$$

Calculating step-by-step:

$$
0.2 \times 9.75 = 1.95
$$

$$
0.5 \times 15.75 = 7.875
$$

$$
z_7 = 1 + 1.95 + 7.875 = 10.825
$$

Applying ReLU:

$$
\max(0, 10.825) = 10.825
$$

So, the final output of the network is:

$$
\boxed{10.825}
$$

### b) calculate the 𝛿 for each neuron in the network.

The loss function is mean squared error:

$$
E = \frac{1}{2} (t - y)^2
$$

Taking the derivative with respect to $ N_7 $:

$$
\delta_7 = \frac{\partial E}{\partial N_7} = (y - t)
$$

Substituting values:

$$
\delta_7 = 10.825 - 1 = 9.825
$$

$$
\delta_5 = \delta_7 \times w_5 = 9.825 \times 0.2 = 1.965
$$

$$
\delta_6 = \delta_7 \times w_6 = 9.825 \times 0.5 = 4.9125
$$

Neuron 5 pools $ (N_1, N_2) $, where the max was $ N_2 = 9.75 $.
So only $ \delta_2 $ receives $ \delta_5 $, while $ \delta_1 = 0 $.

$$
\delta_2 = \delta_5 = 1.965, \quad \delta_1 = 0
$$

Neuron 6 pools $ (N_3, N_4) $, where the max was $ N_4 = 15.75 $.
So only$ \delta_4 $ receives $ \delta_6 $, while $ \delta_3 = 0 $.

$$
\delta_4 = \delta_6 = 4.9125, \quad \delta_3 = 0
$$

Results:

$$
\delta_1 = 0
$$

$$
\delta_2 = 1.965
$$

$$
\delta_3 = 0
$$

$$
\delta_4 = 4.9125
$$

$$
\delta_5 = 1.965
$$

$$
\delta_6 = 4.9125
$$

$$
\delta_7 = 9.825
$$

### c)

$$
N_2 = \text{ReLU}(w_0 + w_1\cdot2 + w_2\cdot3 + w_3\cdot4).
$$

Taking partial derivatives:

$$
\frac{\partial N_2}{\partial w_0} = 1, \quad
\frac{\partial N_2}{\partial w_1} = 2, \quad
\frac{\partial N_2}{\partial w_2} = 3, \quad
\frac{\partial N_2}{\partial w_3} = 4.
$$

Since $N_2 > 0$, the ReLU derivative is 1, so the gradient contribution from $ N_2 $ is:

$$
\frac{\partial E}{\partial w_0} \Big|_{N_2} = \delta_2 \times 1 = 1.965,
$$

$$
\frac{\partial E}{\partial w_1} \Big|_{N_2} = \delta_2 \times 2 = 3.93,
$$

$$
\frac{\partial E}{\partial w_2} \Big|_{N_2} = \delta_2 \times 3 = 5.895,
$$

$$
\frac{\partial E}{\partial w_3} \Big|_{N_2} = \delta_2 \times 4 = 7.86.
$$

Since $ N_4 $ is computed as:

$$
N_4 = \text{ReLU}(w_0 + w_1\cdot4 + w_2\cdot5 + w_3\cdot6).
$$

Taking partial derivatives:

$$
\frac{\partial N_4}{\partial w_0} = 1, \quad
\frac{\partial N_4}{\partial w_1} = 4, \quad
\frac{\partial N_4}{\partial w_2} = 5, \quad
\frac{\partial N_4}{\partial w_3} = 6.
$$

Since $N_4 > 0$, the ReLU derivative is 1, so the gradient contribution from $ N_4 $ is:

$$
\frac{\partial E}{\partial w_0} \Big|_{N_4} = \delta_4 \times 1 = 4.9125,
$$

$$
\frac{\partial E}{\partial w_1} \Big|_{N_4} = \delta_4 \times 4 = 19.65,
$$

$$
\frac{\partial E}{\partial w_2} \Big|_{N_4} = \delta_4 \times 5 = 24.5625,
$$

$$
\frac{\partial E}{\partial w_3} \Big|_{N_4} = \delta_4 \times 6 = 29.475.
$$

Since $w_j$ appears in both $N_2$ and $N_4$, the total gradient for each weight is the sum of both contributions:

$$
\frac{\partial E}{\partial w_0} = 1.965 + 4.9125 = 6.8775,
$$

$$
\frac{\partial E}{\partial w_1} = 3.93 + 19.65 = 23.58,
$$

$$
\frac{\partial E}{\partial w_2} = 5.895 + 24.5625 = 30.4575,
$$

$$
\frac{\partial E}{\partial w_3} = 7.86 + 29.475 = 37.335.
$$

Using the standard gradient descent update rule:

$$
\Delta w_j = -\,\alpha \,\frac{\partial E}{\partial w_j}.
$$

So explicitly:

$$
\Delta w_0 = -\,\alpha \times 6.8775,
$$

$$
\Delta w_1 = -\,\alpha \times 23.58,
$$

$$
\Delta w_2 = -\,\alpha \times 30.4575,
$$

$$
\Delta w_3 = -\,\alpha \times 37.335.
$$

## Q6

1. Feedforward (1 hidden layer, 30 nodes, KK outputs, input dimension DD):
   $\boxed{\text{Parameters} = (30D + 30) + (30K + K) = 30D + 30 + 31K.}$
2.

$$
(5 \times 5 \times 1) + 1 = 26 \text{ parameters}.
$$

$$
26 \times 32 = 832.
$$

$$
(5 \times 5 \times 32) + 1 = 801.
$$

$$
801 \times 64 = 51{,}264.
$$

$$
(3136 \times 1024) + 1024 = 3{,}212{,}288.
$$

$$
(1024 \times 10) + 10 = 10{,}250.
$$

$$
\begin{aligned}
&\text{Conv1: } 832 \\
&\text{Conv2: } 51{,}264 \\
&\text{FC1: } 3{,}212{,}288 \\
&\text{FC2: } 10{,}250 \\
\hline
&\textbf{Total: } 3{,}274{,}634.
\end{aligned}
$$

Thus, the CNN has:

$$
\boxed{3{,}274{,}634 \text{ parameters in total}.}
$$

## Q7

1. **Task Complexity**: Larger filters capture broader context but increase computation; smaller filters learn finer details.
2. **Input Image Size**: Larger images may benefit from larger filters or bigger strides to reduce dimension quickly.
3. **Computational Constraints**: More channels and bigger filters mean more parameters and higher memory/computational cost.
4. **Depth of the Network**: Deeper networks often use smaller filters (e.g., 3×3) and fewer strides in early layers to preserve spatial information.

最后修改：2025 年 07 月 19 日

如果觉得我的文章对你有用，请随意赞赏

44 条评论

mrlovcvihp
October 6th, 2025 at 10:47 am

做了几十年的项目我总结了最好的一个盘（纯干货）

回复
tbmaafiemu
May 23rd, 2025 at 03:16 pm

隐秘王国

回复
pjbregauhv
May 23rd, 2025 at 03:14 pm

摸金校尉观山太保

回复
fqsowpwmnh
May 23rd, 2025 at 03:13 pm

把所有东西带回家

回复
agwegaobbg
May 21st, 2025 at 06:44 am

鬼吹灯之龙岭迷窟

回复
yegcjqwexl
May 21st, 2025 at 06:43 am

护国密探

回复
heqzvhotbw
May 18th, 2025 at 08:02 am

迷途的羔羊

回复
kwtioippiv
May 18th, 2025 at 08:01 am

真爱誓言

回复
aovkxmhaan
May 15th, 2025 at 04:31 pm

真爱誓言

回复
xmqbfnrpen
May 15th, 2025 at 04:30 pm

宝莱坞机器人20重生归来

回复
bpzzzzbhgn
May 15th, 2025 at 04:29 pm

梦之婚礼

回复
yfmzwjyvzf
May 15th, 2025 at 04:28 pm

德克斯特的实验室自大之旅

回复
qrwrzmdrpa
May 15th, 2025 at 04:27 pm

恶魔娜塔丽

回复
zdzaymauur
May 15th, 2025 at 04:05 pm

丹佛圣诞节

回复
ilefqoizbt
May 15th, 2025 at 04:04 pm

四大才子番外之真假唐伯虎

回复
vfypgeigkf
May 15th, 2025 at 04:02 pm

鸳鸯楼惊魂

回复
dxbgiartyx
May 15th, 2025 at 04:01 pm

悟空传

回复
rqyjhvjdey
May 15th, 2025 at 04:00 pm

霹雳玫瑰

回复
avgxbwgnim
May 15th, 2025 at 02:53 pm

相声大电影之我要幸福

回复
qzbzpaxeiw
May 15th, 2025 at 02:52 pm

妖猫传

回复
zhmnrzmlfg
May 15th, 2025 at 02:51 pm

林荫路825号

回复
yhptnbwkus
May 15th, 2025 at 02:49 pm

候燕

回复
gzpxruckxe
May 15th, 2025 at 04:24 am

宇航员恋人

回复
lokmlvvcwd
May 15th, 2025 at 04:21 am

两个爸爸

回复
czfcxvzntb
May 12th, 2025 at 07:29 am

阿赫德的膝盖

回复
phlrdtiujq
May 12th, 2025 at 07:28 am

css教程

回复
ovyvkrejao
May 12th, 2025 at 07:26 am

优雅的相遇

回复
pzcaeoiaay
May 12th, 2025 at 07:24 am

战锋尖峰对决

回复
plxfznhrpj
May 12th, 2025 at 07:23 am

有趣页面

回复
fsecpdpgrb
May 9th, 2025 at 09:23 pm

我要我们在一起

回复
tjuxtsknpb
May 9th, 2025 at 09:22 pm

芝拉克

回复
tstlavmdxy
May 9th, 2025 at 09:20 pm

金鱼

回复
ipldhvgiwk
May 9th, 2025 at 09:18 pm

乒乓

回复
vtmutymqor
May 9th, 2025 at 08:54 pm

第三将来时

回复
vqmfmkcamf
May 9th, 2025 at 08:53 pm

总是有爱在隔离粤配

回复
vdmuvwuifc
May 9th, 2025 at 08:51 pm

终极斗士

回复
eejhrfaept
May 9th, 2025 at 08:50 pm

库德拉特

回复
ixzfeagtiv
May 9th, 2025 at 08:49 pm

身骄肉贵

回复
kbgeymgkvd
May 9th, 2025 at 08:48 pm

五郎八卦棍粤配

回复
ximddxupde
May 4th, 2025 at 05:15 am

彩虹

回复
ujjaqucqgo
May 4th, 2025 at 05:13 am

摸金校尉观山太保

回复
dfpdoitxht
May 4th, 2025 at 05:12 am

快乐赢家

回复
vgmaijycae
May 4th, 2025 at 05:10 am

倚天屠龙记之九阳神功

回复
hnpnuycgcf
May 4th, 2025 at 05:09 am

燃烧

回复

发表评论取消回复
使用cookie技术保留您的个人信息以便您下次快速评论，继续评论表示您已同意该条款

评论 *

私密评论

名称 *

🎲

邮箱 *

地址

SYSC5108_A3

William.W • 2025 年 03 月 06 日